Loudspeaker SPL Expectations and Reality

by Ivan Beaver

There is a lot of confusion concerning loudspeakers and how much SPL they will produce.  We will look at a few of the situations and hopefully try to clear up a few misconceptions.

Because audio is very dynamic, it is hard to assign a single simple number.  It IS important to understand what the variables are, how they interact, the differences, and so forth, in order to start to gain a reasonable understanding of how loud or the SPL that it is producing.

In this article, we will only be concerned with the flat or Z SPL.  A and C scales are weighted with respect to frequency response and for specific reasons.  However, that is beyond the scope of this discussion and for another tech topic.

People often ask: “How loud will this loudspeaker get?”  That is the question; HOWEVER, that is not what they really want to know.  What they want to know is, “How loud will that loudspeaker get WHILE STILL SOUNDING DECENT?”  That is a completely different question, with a different answer, and not the one they want to hear.

Let’s backtrack a little bit and go to some basics.  Loudspeaker SPL is usually referenced to 1m. Some other distances have been used in the past, for the same reason/purpose, you just need to know the specific distance and applied signal level and SPL reading.  The reason for this is to be able to calculate how loud it will be at some other distance, using inverse square law.

The formula is:  dB difference=20xlog(D1/D2).  Where D is the 1meter (or other known distance) and the distance of interest.  You then subtract that number from the SPL capability (a combination of sensitivity and power capacity) of the 1m distance.  Yes, the formula can change a bit with large arrays, but we will keep it simple for a single cabinet for this discussion.

This information helps to design a loudspeaker system that will provide adequate/expected SPLs at a specific distance away from the loudspeaker.

That is good, but what SPL number do we use to “subtract” from?  Is it a simple number on a spec sheet?  Where did that number come from?  Does that number represent the full range of frequencies that the loudspeaker will produce or a single peak?  How was it measured or was it just calculated?  What was the basis of the calculation?  All of these can produce varying answers (sometimes over a wide range), and without knowing where the number comes from, your expected SPL at a certain distance could be way off. Let us now look at a few of the variances and where some of the numbers come from.

Test Signals

Various test signals contain different crest factors, and different frequency responses (most standards are not flat).  The crest factor is basically the ratio of the peak part of the signal to the “average” levels. A ratio of 6dB is the same as a power factor of 4x. This means an amplifier that is producing 100 watts continuous, must be able to produce 400 watts for the peaks.  A crest factor of 12dB (closer to actual music) has a power ratio of 16x. That same 100 watt amplifier must be able to produce 1600 watts for the peaks.   Since 15dB is a good median crest factor, that same 100 watt amplifier needs to be able to produce 3200 watts in order to pass the peaks cleanly and accurately.

There are a couple of test signals used for loudspeaker driver power ratings.  Among them are AES, IEC, EIA. It is beyond the scope of this topic to dive into the differences between them, but suffice it to say they are all trying to do the same thing-determine how much power/voltage a loudspeaker can handle (they all follow the same basic ideas, but with variances). Which is not an easy task, as audio is very dynamic.  The only thing that these various signals tell you are that a loudspeaker can withstand a specific input (calculated wattage) for a specific time period and not be damaged. They give NO indication as to what the loudspeaker sounds like, how much distortion or noise etc is being produced, just that it won’t be damaged by that signal at the rated power applied (how that power is calculated can also vary a bit)

Generally, the wattage capacity is stated as any of the following: continuous (sometimes called RMS), program (sometimes called music power), peak, with their being a 6dB difference between the continuous and the peak ratings.  The term “peak” is one that has different meanings to different people, but that is another topic.  So there could be a 9dB difference between continuous and peak.

The frequency response graph can be a good indicator of how loud particular frequencies will be with regard to others with a given input voltage.  It is usually associated with a specific input voltage (2.83V for 1 watt @ 8 ohms).  It should be with no processing applied (assuming a passive loudspeaker).  With active or self-powered you need to look at each band individually.   If you apply any processing (boosting or cutting), then the applied voltage will be different (higher or lower) for those affected frequencies.  This can be deceiving of how much SPL the loudspeaker can produce, based on the wattage capability.  For example: if a 6dB boost is applied to the low frequencies, then you MUST subtract that 6dB from the loudspeaker’s maximum SPL capability at those frequencies, because those frequencies were getting a higher signal level, ie more wattage.

The usual method for calculating SPLs from the frequency response graph is (or should be) as follows.  First, determine the “middle ground” SPL from the graph.  This could be called an average of the peaks and dips in the response.  Now determine the wattage gain (based on the applied wattage/voltage for the graph) and the power capacity of the loudspeaker.  Assume you have a 1000 watt rated continuous and the nominal impedance is 4 ohms, with a sensitivity of 98dB with an applied voltage of 2.83V.  You do not apply power to a loudspeaker, only voltage.  The resultant power will be different at different frequencies, depending on the actual impedance at those frequencies.

Since 4 ohms is 2 watts at 2.83V, you would use the following formula:

SPL power increase=10log(1000/2).    The 1000 is the continuous rated power.  This yields a power gain of 27dB.

You simply add 27dB to the sensitivity rating (in this case 98dB) and you get 125dB continuous SPL.  You can then add 6dB (because of the crest factor in the test signal) to that for the peak rating, 131dB SPL.

You will never measure both the continuous and peak specs when playing music. It is either the peak OR the continuous, but never both (except for a few musical passages). Normal music is much more dynamic than the test signal.  Typically around 15dB.  So while the loudspeaker may be producing the peaks (an average lower cost SPL meter cannot read the short peak SPLs, the “maximum” on those meters is also not a peak reading, just a maximum of the slower response), the continuous levels (that you would read on an average consumer SPL meter) are most likely going to be around 15dB lower.  So while the spec sheet may say 125dB continuous,  you may only read around 115dB, and then only at 1 meter or equivalent (with distance loses).  The above math assumes a 131dB peak and dynamic range of around 15-16dB.

Sensitivity

This number needs to come from the USABLE sensitivity of the loudspeaker, not something out of the intended frequency range of usage, or a large peak in the response.  If based on one of those, then the actual SPL when being used will be less than expected.  Here are two real-world examples of knowing where the peak is measured, which makes a big difference in what can realistically be expected in terms of SPL from the loudspeaker cabinet.

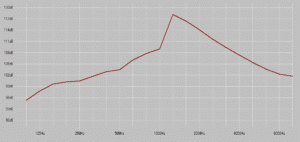
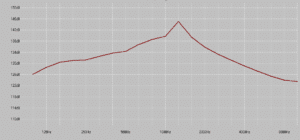
In the first example, it is a popular 2 way loudspeaker with a 2” exit compression driver. It is rated at 143dB maximum output.  You can see from the sensitivity in the first graph, that there is a peak in the response around 1300Hz (which is to be expected from a 2” exit driver on a decent sized horn).  In the second graph, you can see the maximum output of each freq (based on 1/3^rd oct steps).

So while although the cabinet can produce 143dB SPL, it can only do so over a very limited freq range (the peak around 1300Hz), however the overall maximum output is around 10dB lower.  Nobody would ever listen to the cabinet with that peak, especially at those levels.

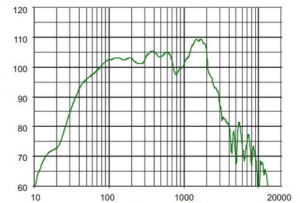
The next example is a subwoofer.  It has a rated sensitivity of 108dB 20Hz-20KHz.  As you can see, there is a range in which the cabinet does have a sensitivity of 108dB, but it is not even close to the frequency range in which the cabinet will be used.  It is around 1300Hz-1900Hz.  If you look at the freq range in which the cabinet will be typically used (it is a subwoofer, so below 80 or 90Hz), the sensitivity is about 10dB or more lower in the 40-50-60Hz range.  So while the sub can produce much higher (again around 10dB) peak SPLs, it is not within the intended operating range of interest.  Therefore the usable output is much lower than a simple number on the spec sheet would suggest.

Very often the peak SPL numbers are calculated (as described above), but that does not always give a good indication of how loud the cabinet can actually get across the intended frequency spectrum, and still be listenable.

M Noise

There is a relatively new test signal that has been developed (and standards are being worked on) to show the loudspeakers maximum linear SPL.  Which if done correctly, can give a good idea of the maximum continuous and peak SPLs that could be expected from the loudspeaker and should be comparable between different manufacturers and models of loudspeakers.  It is a much better method than the old calculated methods and should produce more comparable and accurate results.

We will not get into the details or parameters of the actual measurements in this article.  That is beyond the scope.

It is called M noise.  It has the musical intensity shape of the other test signals on the higher frequencies, but the lower frequencies are flat with m noise, vs being rolled off on previous test signals, which gives a more realistic representation of modern music, but the main difference is that the crest factor varies with frequency.  Basically, the crest factor gets greater as the frequency rises. Below 500hz, the crest factor is the same as previous signals (12dB).  It also reaches a higher crest factor (17dB) which closely resembles the actual dynamic range of most music.  It is not for testing how much signal a loudspeaker can withstand before damage, but rather how much SPL a loudspeaker can produce while still sounding musical.  So the M noise specs will often be lower than a “maximum power” spec.

Sounding good can be subjective, and there are two “stop points” in the M noise measuring procedure.  M noise is measured, not calculated, so it is much more realistic and repeatable.  Whenever either of the two stop points is reached, the level is no longer increased, and the SPL is measured.  One of the stop points is power compression.  This occurs when the SPL produced by the loudspeaker is no longer increasing by the same amount as the incoming signal.  The limit is 2dB, so it is barely audible, but easily measured.  The other stop point is distortion.  It is measured by using the coherence of the signal (basically measuring the signal to noise ratio) and when it gets down to 10dB SNR the level is no longer increased.  The noise in this case would often be the distortion or other artifacts produced by the loudspeaker.

In either stop condition, the loudspeaker would be considered to be no longer linear in its response at that point.  Ie “musical” and reproduction is accurate.

The actual SPL may or may not be measured at 1m (it should be in the far-field of the loudspeaker), but is always referenced to 1m.  In the case of some larger loudspeakers, an actual 1m measurement is not representative of the level that would be used for distance calculations.  It could be higher or lower.  In those larger cabinets, the SPL measurement is made at a further distance (the far-field) and then back-calculated to the 1m equivalent.  This is a total viable and accepted method because it is actually measured at that further distance.

The M noise method is good for both powered and nonpowered loudspeakers.

In conclusion, when looking at how loud a loudspeaker can get, there are many things that must be considered, other than a simple number on a spec sheet.  Try to understand where the numbers came from, and how they can be misused or misunderstood.

Remember that is not just how loud it can get (a piece of metal through a table saw is REALLY loud), but how loud it can get while still sounding good that is important.